Tierra y cielo

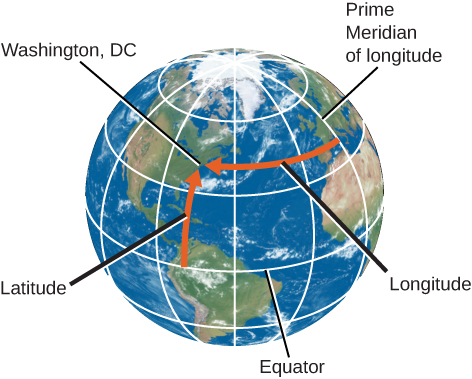
Localización de lugares en la Tierra
Empecemos por fijar nuestra posición en la superficie del planeta Tierra. Como ya comentamos en Observar el cielo: el nacimiento de la astronomía, el eje de rotación de la Tierra define la ubicación de sus polos norte y sur y de su ecuador, a medio camino entre ambos. Otras dos direcciones también están definidas por los movimientos de la Tierra: el este es la dirección hacia la que gira la Tierra, y el oeste es su opuesto. En casi cualquier punto de la Tierra, las cuatro direcciones -norte, sur, este y oeste- están bien definidas, a pesar de que nuestro planeta es redondo y no plano. Las únicas excepciones se encuentran exactamente en los polos norte y sur, donde las direcciones este y oeste son ambiguas (porque los puntos situados exactamente en los polos no giran).

Podemos utilizar estas ideas para definir un sistema de coordenadas vinculado a nuestro planeta. Un sistema así, como el trazado de calles y avenidas en Manhattan o Salt Lake City, nos ayuda a encontrar dónde estamos o a dónde queremos ir. Sin embargo, las coordenadas en una esfera son un poco más complicadas que las de una superficie plana. Debemos definir círculos en la esfera que desempeñen el mismo papel que la cuadrícula rectangular que vemos en los mapas de las ciudades.

Cualquier punto de la superficie de la Tierra tendrá un meridiano que pase por él (Figura 4.2). El meridiano especifica la ubicación este-oeste, o longitud, del lugar. Por acuerdo internacional (y fueron necesarias muchas reuniones para que los países del mundo se pusieran de acuerdo), la longitud se define como el número de grados de arco a lo largo del ecuador entre tu meridiano y el que pasa por Greenwich, Inglaterra, que ha sido designado como el Primer Meridiano. La longitud del primer meridiano se define como 0°.

¿Por qué Greenwich? Todos los países querían que la longitud 0° pasara por su propia capital. Se eligió Greenwich, sede del antiguo Real Observatorio (figura 4.3), porque estaba entre Europa continental y Estados Unidos, y porque allí se desarrolló gran parte del método para medir la longitud en el mar. Las longitudes se miden al este o al oeste del meridiano de Greenwich, de 0° a 180°. Por ejemplo, la longitud del punto de referencia de la casa del reloj del Observatorio Naval de Estados Unidos en Washington, DC, es 77,066° O.

Tu latitud (o ubicación norte-sur) es el número de grados de arco que te separan del ecuador a lo largo de tu meridiano. Las latitudes se miden al norte o al sur del ecuador, de 0° a 90°. (La latitud del ecuador es 0°.) Como ejemplo, la latitud del punto de referencia del Observatorio Naval mencionado anteriormente es 38,921° N. La latitud del Polo Sur es 90° S, y la latitud del Polo Norte es 90° N.

Localización de lugares en el cielo
Las posiciones en el cielo se miden de forma muy similar a como se miden las posiciones en la superficie de la Tierra. Sin embargo, en lugar de latitud y longitud, los astrónomos utilizan unas coordenadas denominadas declinación y ascensión recta. Para indicar las posiciones de los objetos en el cielo, a menudo es conveniente utilizar la esfera celeste ficticia. En Observación del cielo: el nacimiento de la astronomía vimos que el cielo parece girar en torno a unos puntos situados sobre los polos norte y sur de la Tierra, puntos del cielo denominados polo norte celeste y polo sur celeste. A medio camino entre los polos celestes, y por tanto a 90° de cada polo, se encuentra el ecuador celeste, un gran círculo de la esfera celeste que está en el mismo plano que el ecuador de la Tierra. Podemos utilizar estas marcas en el cielo para establecer un sistema de coordenadas celestes.

La declinación en la esfera celeste se mide del mismo modo que la latitud en la esfera terrestre: desde el ecuador celeste hacia el norte (positiva) o hacia el sur (negativa). Así, Polaris, la estrella cercana al polo norte celeste, tiene una declinación de casi +90°.

La ascensión recta (AD) es como la longitud, salvo que, en lugar de Greenwich, el punto elegido arbitrariamente para empezar a contar es el equinoccio de primavera, un punto del cielo en el que la eclíptica (la trayectoria del Sol) cruza el ecuador celeste. El AR puede expresarse en unidades de ángulo (grados) o en unidades de tiempo. Esto se debe a que la esfera celeste parece girar alrededor de la Tierra una vez al día, a medida que nuestro planeta gira sobre su eje. Por lo tanto, los 360° de AR que se tarda en dar una vuelta a la esfera celeste pueden equivaler a 24 horas. Entonces, cada 15° de arco equivale a 1 hora de tiempo. Por ejemplo, las coordenadas celestes aproximadas de la estrella brillante Capella son AR 5h = 75° y declinación +50°.

Una forma de visualizar estos círculos en el cielo es imaginar la Tierra como una esfera transparente con las coordenadas terrestres (latitud y longitud) pintadas en ella con pintura oscura. Imagina la esfera celeste que nos rodea como una bola gigante, pintada de blanco por dentro. Luego imagínate en el centro de la Tierra, con una bombilla brillante en el centro, mirando al cielo a través de su superficie transparente. Los polos terrestres, el ecuador y los meridianos se proyectarán como sombras oscuras sobre la esfera celeste, dándonos el sistema de coordenadas en el cielo.

La Tierra que gira
¿Por qué salen y se ponen muchas estrellas cada noche? ¿Por qué, en otras palabras, el cielo nocturno parece girar? Hemos visto que la rotación aparente de la esfera celeste podría explicarse por una rotación diaria del cielo alrededor de una Tierra inmóvil o por la rotación de la propia Tierra. Desde el siglo XVII, se acepta generalmente que es la Tierra la que gira, pero hasta el siglo XIX el físico francés Jean Foucault no aportó una demostración inequívoca de esta rotación. En 1851, suspendió un péndulo de 60 metros y unos 25 kilogramos de peso de la cúpula del Panteón de París y lo hizo oscilar uniformemente.