Astronomía antigua

Volvamos ahora brevemente la vista atrás en la historia. Gran parte de la civilización occidental moderna se deriva, de un modo u otro, de las ideas de los antiguos griegos y romanos, y esto también es cierto en el caso de la astronomía. Sin embargo, muchas otras culturas antiguas también desarrollaron sofisticados sistemas de observación e interpretación del cielo.

 

 

Astronomía en el mundo
Los antiguos astrónomos babilonios, asirios y egipcios conocían la duración aproximada del año. Los egipcios de hace 3.000 años, por ejemplo, adoptaron un calendario basado en un año de 365 días. Llevaban un cuidadoso seguimiento de la hora de salida de la brillante estrella Sirio en el cielo antes del amanecer, que tiene un ciclo anual que se corresponde con la crecida del río Nilo. Los chinos también tenían un calendario funcional; determinaban la duración del año más o menos al mismo tiempo que los egipcios. Los chinos también registraban cometas, meteoros brillantes y manchas oscuras en el Sol. (Muchos tipos de objetos astronómicos se presentaron en La ciencia y el universo: Un breve recorrido. Si no estás familiarizado con términos como cometas y meteoritos, quizá quieras repasar ese capítulo). Más tarde, los astrónomos chinos llevaron un cuidadoso registro de las "estrellas invitadas", es decir, aquellas que normalmente son demasiado débiles para verlas pero que de repente se iluminan y se hacen visibles a simple vista durante unas semanas o meses. Todavía utilizamos algunos de estos registros para estudiar estrellas que explotaron hace mucho tiempo.

La cultura maya de México y América Central desarrolló un sofisticado calendario basado en el planeta Venus, y realizaba observaciones astronómicas desde lugares dedicados a este fin hace mil años. Los polinesios aprendieron a navegar por las estrellas a lo largo de cientos de kilómetros de océano abierto, una habilidad que les permitió colonizar nuevas islas muy lejos de donde empezaron.

Cosmología griega y romana
Nuestro concepto del cosmos -su estructura básica y su origen- se denomina cosmología, palabra de raíz griega. Antes de la invención de los telescopios, los humanos tenían que depender de la simple evidencia de sus sentidos para hacerse una idea del universo. Los antiguos desarrollaron cosmologías que combinaban su visión directa de los cielos con una rica variedad de simbolismos filosóficos y religiosos.

 

Al menos 2.000 años antes de Colón, los pueblos cultos del Mediterráneo oriental sabían que la Tierra era redonda. La creencia en una Tierra esférica puede tener su origen en la época de Pitágoras, filósofo y matemático que vivió hace 2.500 años. Creía que los círculos y las esferas eran "formas perfectas" y sugirió que la Tierra debía ser, por tanto, una esfera. Como prueba de que a los dioses les gustaban las esferas, los griegos citaron el hecho de que la Luna es una esfera, utilizando pruebas que describiremos más adelante.

Los escritos de Aristóteles (384-322 a.C.), tutor de Alejandro Magno, resumen muchas de las ideas de su época. En ellos se describe cómo la progresión de las fases de la Luna -su aparente cambio de forma- se debe a que vemos distintas partes del hemisferio de la Luna iluminado por el Sol a medida que transcurre el mes (véase Tierra, Luna y Cielo). Aristóteles también sabía que el Sol tiene que estar más lejos de la Tierra que la Luna porque, en ocasiones, la Luna pasa exactamente entre la Tierra y el Sol y lo oculta temporalmente. A esto lo llamamos eclipse solar.

Aristóteles citó argumentos convincentes de que la Tierra debe ser redonda. El primero es el hecho de que cuando la Luna entra o sale de la sombra de la Tierra durante un eclipse de Luna, la forma de la sombra que se ve en la Luna es siempre redonda (figura 2.9). Sólo un objeto esférico produce siempre una sombra redonda. Si la Tierra fuera un disco, por ejemplo, habría algunas ocasiones en las que la luz solar incidiría de canto sobre ella y su sombra sobre la Luna sería una línea.

Como segundo argumento, Aristóteles explicó que los viajeros que recorren una distancia considerable hacia el sur pueden observar estrellas que no son visibles más al norte. Y la altura de la Estrella Polar -la estrella más cercana al polo norte celeste- disminuye a medida que el viajero se desplaza hacia el sur. En una Tierra plana, todo el mundo vería las mismas estrellas. La única explicación posible es que el viajero debe haberse desplazado sobre una superficie curva de la Tierra, mostrando las estrellas desde un ángulo diferente. (Véase el artículo ¿Cómo sabemos que la Tierra es redonda? para más ideas sobre cómo demostrar que la Tierra es redonda).

FUNDAMENTOS DE ASTRONOMÍA
¿Cómo sabemos que la Tierra es redonda?
Además de las dos formas (a partir de los escritos de Aristóteles) comentadas en este capítulo, también podrías razonar de la siguiente manera:

Observemos un barco que sale de su puerto y navega en la distancia en un día despejado. En una Tierra plana, veríamos que el barco se hace cada vez más pequeño a medida que se aleja. Pero esto no es lo que observamos en realidad. En cambio, los barcos se hunden bajo el horizonte, desapareciendo primero el casco y permaneciendo visible el mástil durante algún tiempo más. Al final, sólo se ve la parte superior del mástil mientras el barco navega alrededor de la curvatura de la Tierra. Finalmente, el barco desaparece bajo el horizonte.
La Estación Espacial Internacional da una vuelta a la Tierra cada 90 minutos aproximadamente. Las fotografías tomadas desde el transbordador y otros satélites muestran que la Tierra es redonda desde cualquier perspectiva.
El Sol está tan lejos de nosotros que todos los rayos de luz que inciden en nuestro planeta se acercan siguiendo líneas esencialmente paralelas. Para ver por qué, observe la Figura 2.10. Tomemos una fuente de luz cercana a la Tierra, por ejemplo, en la posición A. Sus rayos inciden en distintas partes de la Tierra siguiendo trayectorias divergentes. Desde una fuente de luz situada en B, o en C (que está aún más lejos), el ángulo entre los rayos que inciden en partes opuestas de la Tierra es menor. Cuanto más alejada esté la fuente, menor será el ángulo entre los rayos. Para una fuente infinitamente lejana, los rayos se desplazan a lo largo de líneas paralelas.

 

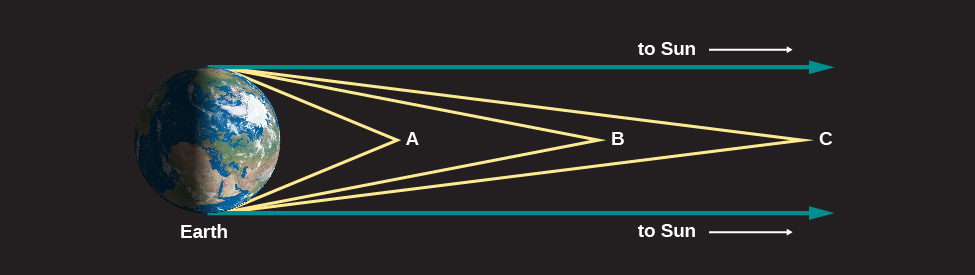
Por supuesto, el Sol no está infinitamente lejos, pero dada su distancia de 150 millones de kilómetros, los rayos de luz que inciden en la Tierra desde un punto del Sol divergen entre sí en un ángulo demasiado pequeño para ser observado a simple vista. En consecuencia, si las personas de toda la Tierra que pudieran ver el Sol lo apuntaran, sus dedos estarían esencialmente paralelos entre sí. (Lo mismo ocurre con los planetas y las estrellas, una idea que utilizaremos en nuestra discusión sobre el funcionamiento de los telescopios).

 

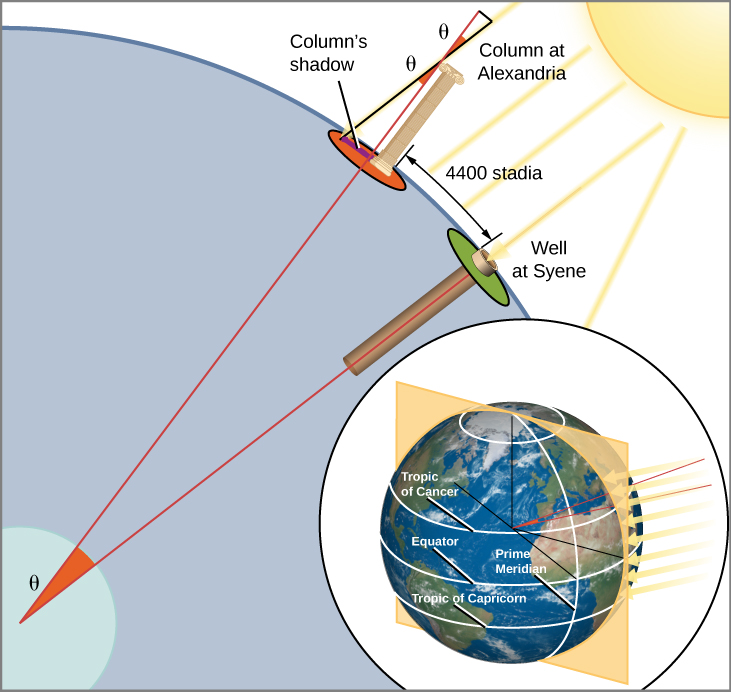
No es posible evaluar con precisión la exactitud de la solución de Eratóstenes porque existen dudas sobre cuál de los diversos tipos de estadios griegos utilizó como unidad de distancia. Si fue el estadio olímpico común, su resultado es aproximadamente 20% demasiado grande. Según otra interpretación, utilizó un estadio equivalente a 1/6 de kilómetro, en cuyo caso su cifra estaba a 1% del valor correcto de 40.000 kilómetros. Aunque su medición no fuera exacta, su éxito al medir el tamaño de nuestro planeta utilizando únicamente las sombras, la luz solar y el poder del pensamiento humano fue uno de los mayores logros intelectuales de la historia.

Hiparco y la Precesión
Quizá el mayor astrónomo de la Antigüedad fue Hiparco, nacido en Nicea, en la actual Turquía. Erigió un observatorio en la isla de Rodas hacia el año 150 a.C., cuando la República Romana estaba expandiendo su influencia por la región mediterránea. Allí midió, con la mayor precisión posible, las posiciones de los objetos en el cielo, compilando un catálogo estelar pionero con unas 850 entradas. Designó coordenadas celestes para cada estrella, especificando su posición en el cielo, igual que nosotros especificamos la posición de un punto en la Tierra dando su latitud y longitud.

También dividió las estrellas en magnitudes aparentes según su brillo aparente. Llamó a las más brillantes "estrellas de primera magnitud"; al siguiente grupo más brillante, "estrellas de segunda magnitud"; y así sucesivamente. Este sistema bastante arbitrario, en su forma modificada, sigue utilizándose hoy en día (aunque cada vez es menos útil para los astrónomos profesionales).

 

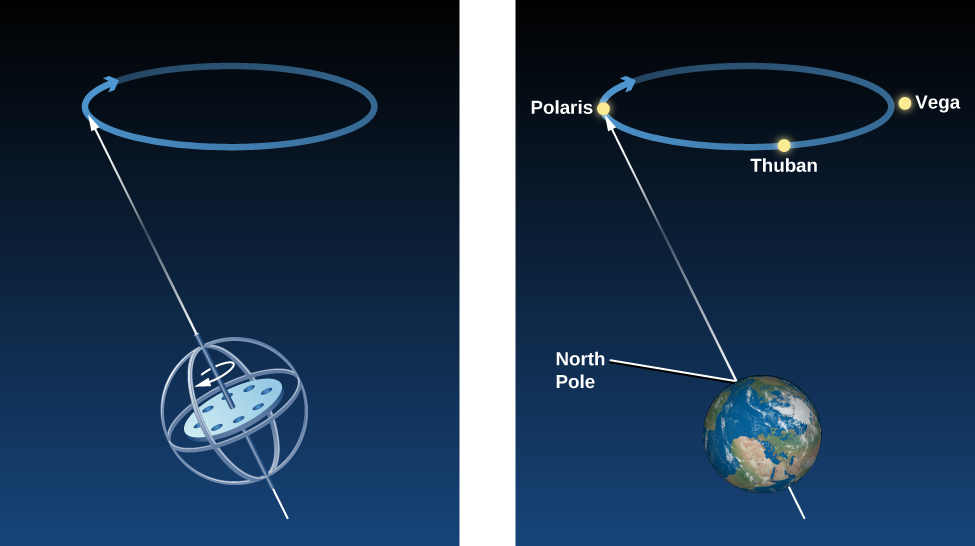
Como nuestro planeta no es una esfera exacta, sino que se abomba un poco en el ecuador, los tirones del Sol y la Luna hacen que se tambalee como una peonza. El eje de la Tierra tarda unos 26.000 años en completar una vuelta de precesión. Como consecuencia de este movimiento, el punto al que apunta nuestro eje en el cielo cambia con el paso del tiempo. Mientras que Polaris es la estrella más cercana al polo norte celeste en la actualidad (alcanzará su punto más cercano hacia el año 2100), la estrella Vega, en la constelación de Lyra, será la estrella polar dentro de 14.000 años.

El modelo del Sistema Solar de Ptolomeo
El último gran astrónomo de la época romana fue Claudio Ptolomeo (o Ptolomeo), que floreció en Alejandría hacia el año 140. Escribió una gigantesca compilación de conocimientos astronómicos que hoy se conoce con el nombre árabe de Almagesto (que significa "El más grande"). Escribió una gigantesca compilación de conocimientos astronómicos, que hoy se conoce por su nombre árabe, Almagest (que significa "El más grande"). El Almagesto no trata exclusivamente de la obra de Ptolomeo, sino que incluye un análisis de los logros astronómicos del pasado, principalmente los de Hiparco. Hoy en día, es nuestra principal fuente de información sobre la obra de Hiparco y otros astrónomos griegos.

La aportación más importante de Ptolomeo fue una representación geométrica del sistema solar que predecía las posiciones de los planetas para cualquier fecha y hora deseadas. Hiparco, que no disponía de datos suficientes para resolver el problema por sí mismo, había reunido material de observación para la posteridad. Ptolomeo complementó este material con nuevas observaciones propias y elaboró un modelo cosmológico que perduró más de mil años, hasta la época de Copérnico.

El factor que complica la explicación de los movimientos de los planetas es que su aparente vagabundeo en el cielo resulta de la combinación de sus propios movimientos con la revolución orbital de la Tierra. Cuando observamos los planetas desde nuestro punto de vista en la Tierra en movimiento, es un poco como ver una carrera de coches mientras estás compitiendo en ella. A veces, los coches de los contrincantes te adelantan, pero otras veces tú les adelantas a ellos, lo que hace que durante un rato parezca que retroceden con respecto a ti.

La figura 2.13 muestra el movimiento de la Tierra y de un planeta más alejado del Sol, en este caso Marte. La Tierra gira alrededor del Sol en la misma dirección que el otro planeta y casi en el mismo plano, pero su velocidad orbital es mayor. Como resultado, adelanta al planeta periódicamente, como un coche de carreras más rápido en la pista interior. La figura muestra dónde vemos el planeta en el cielo en diferentes momentos. La trayectoria del planeta entre las estrellas se ilustra en el campo estelar de la parte derecha de la figura.