Las leyes del movimiento planetario

Observatorio Tycho Brahe
Tres años después de la publicación del De Revolutionibus de Copérnico, Tycho Brahe nació en el seno de una familia de la nobleza danesa. Desde muy joven se interesó por la astronomía y realizó importantes observaciones astronómicas. Entre ellas, un minucioso estudio de lo que hoy sabemos que era una estrella en explosión que brillaba con gran fulgor en el cielo nocturno.

 

En Hven, Brahe realizó un registro continuo de las posiciones del Sol, la Luna y los planetas durante casi 20 años. Sus amplias y precisas observaciones le permitieron observar que las posiciones de los planetas variaban con respecto a las indicadas en las tablas publicadas, que se basaban en la obra de Ptolomeo. Estos datos eran extremadamente valiosos, pero Brahe no tenía la capacidad de analizarlos y desarrollar un modelo mejor que el que había publicado Ptolomeo. Además, se sentía cohibido porque era un tipo extravagante y cascarrabias, y acumuló enemigos entre los funcionarios del gobierno. Cuando su mecenas, Federico II, murió en 1597, Brahe perdió su base política y decidió abandonar Dinamarca. Se instaló en Praga, donde se convirtió en astrónomo de la corte del emperador Rodolfo de Bohemia. Allí, el año anterior a su muerte, Brahe encontró a un joven matemático muy capaz, Johannes Kepler, para que le ayudara a analizar sus extensos datos planetarios.

Johannes Kepler
Johannes Kepler nació en el seno de una familia pobre de la provincia alemana de Wurtemberg y vivió gran parte de su vida en medio de la agitación de la Guerra de los Treinta Años (véase la figura 3.2). Asistió a la universidad en Tubinga y estudió la carrera de teología. Allí aprendió los principios del sistema copernicano y se convirtió a la hipótesis heliocéntrica. Finalmente, Kepler se trasladó a Praga para trabajar como ayudante de Brahe, quien le puso a trabajar para encontrar una teoría satisfactoria del movimiento planetario que fuera compatible con la larga serie de observaciones realizadas en Hven. Brahe era reacio a proporcionar mucho material a Kepler en un momento dado por miedo a que éste descubriera por sí mismo los secretos del movimiento universal, robándole así a Brahe parte de la gloria. Sólo después de la muerte de Brahe, en 1601, Kepler obtuvo la plena posesión de los valiosísimos registros. Su estudio ocupó la mayor parte del tiempo de Kepler durante más de 20 años.

Las dos primeras leyes del movimiento planetario
La trayectoria de un objeto a través del espacio se denomina órbita. Kepler supuso inicialmente que las órbitas de los planetas eran círculos, pero hacerlo no le permitió encontrar órbitas que concordaran con las observaciones de Brahe. Trabajando con los datos de Marte, acabó descubriendo que la órbita de ese planeta tenía la forma de un círculo algo achatado, o elipse. Junto con el círculo, la elipse es el tipo de curva cerrada más simple, perteneciente a una familia de curvas conocidas como secciones cónicas (Figura 3.3).

 

 

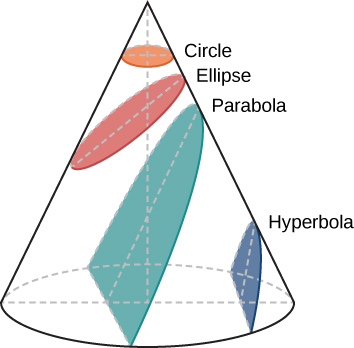
Quizá recuerdes de las clases de matemáticas que, en una circunferencia, el centro es un punto especial. La distancia desde el centro a cualquier punto del círculo es exactamente la misma. En una elipse, la suma de las distancias desde dos puntos especiales del interior de la elipse a cualquier punto de la elipse es siempre la misma. Estos dos puntos del interior de la elipse se denominan focos, palabra inventada por Kepler.

Esta propiedad sugiere una forma sencilla de dibujar una elipse (Figura 3.4). Enrollamos los extremos de un lazo de cuerda alrededor de dos chinchetas introducidas a través de una hoja de papel en un tablero de dibujo, de modo que la cuerda quede floja. Si empujamos un lápiz contra la cuerda, tensándola, y luego deslizamos el lápiz contra la cuerda alrededor de las chinchetas, la curva resultante es una elipse. En cualquier punto donde se encuentre el lápiz, la suma de las distancias del lápiz a las dos chinchetas es una longitud constante: la longitud de la cuerda. Las chinchetas están en los dos focos de la elipse.

 

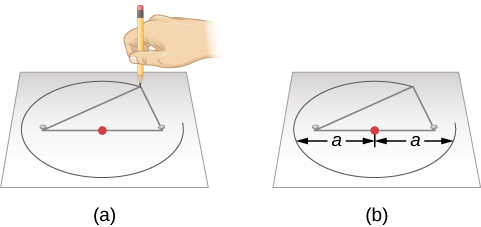
La forma (redondez) de una elipse depende de la distancia entre los dos focos y el eje mayor. La relación entre la distancia entre los focos y la longitud del eje mayor se denomina excentricidad de la elipse.

Si los focos (o tachuelas) se desplazan al mismo lugar, entonces la distancia entre los focos sería cero. Esto significa que la excentricidad es cero y que la elipse no es más que un círculo; por tanto, una circunferencia puede denominarse elipse de excentricidad cero. En un círculo, el semieje mayor sería el radio.

A continuación, podemos hacer elipses de varias elongaciones (o longitudes extendidas) variando el espaciado de las tachuelas (siempre que no estén más separadas que la longitud de la cuerda). Cuanto mayor sea la excentricidad, más alargada será la elipse, hasta una excentricidad máxima de 1,0, cuando la elipse se vuelve "plana", el otro extremo de un círculo.

El tamaño y la forma de una elipse están completamente especificados por su semieje mayor y su excentricidad. Utilizando los datos de Brahe, Kepler descubrió que Marte tiene una órbita elíptica, con el Sol en un foco (el otro foco está vacío). La excentricidad de la órbita de Marte es de sólo 0,1 aproximadamente; su órbita, dibujada a escala, sería prácticamente indistinguible de un círculo, pero la diferencia resultó ser crítica para comprender los movimientos planetarios.

La segunda ley de Kepler trata de la velocidad con la que cada planeta se desplaza a lo largo de su elipse, también conocida como velocidad orbital. A partir de las observaciones de Brahe sobre Marte, Kepler descubrió que el planeta se acelera al acercarse al Sol y se ralentiza al alejarse de él. Expresó la forma precisa de esta relación imaginando que el Sol y Marte están conectados por una línea recta y elástica. Cuando Marte está más cerca del Sol (posiciones 1 y 2 en la figura 3.5), la línea elástica no se estira tanto y el planeta se mueve rápidamente. Más lejos del Sol, como en las posiciones 3 y 4, la línea se estira mucho y el planeta no se mueve tan rápido. A medida que Marte se desplaza en su órbita elíptica alrededor del Sol, la línea elástica barre zonas de la elipse a medida que se mueve (las regiones coloreadas en nuestra figura). Kepler descubrió que, en intervalos iguales de tiempo (t), las áreas barridas en el espacio por esta línea imaginaria son siempre iguales; es decir, el área de la región B de 1 a 2 es la misma que la de la región A de 3 a 4.

Si un planeta se mueve en una órbita circular, la línea elástica se estira siempre lo mismo y el planeta se mueve a una velocidad constante alrededor de su órbita. Pero, como descubrió Kepler, en la mayoría de las órbitas esa velocidad de un planeta que orbita alrededor de su estrella (o de una luna que orbita alrededor de su planeta) tiende a variar porque la órbita es elíptica.

 

 

Tercera ley de Kepler
Las dos primeras leyes del movimiento planetario de Kepler describen la forma de la órbita de un planeta y permiten calcular la velocidad de su movimiento en cualquier punto de la órbita. A Kepler le complacía haber descubierto estas reglas fundamentales, pero no satisfacían su afán por comprender plenamente los movimientos planetarios. Quería saber por qué las órbitas de los planetas estaban espaciadas como lo están y encontrar un patrón matemático en sus movimientos, una "armonía de las esferas", como él la llamaba. Durante muchos años trabajó para descubrir las relaciones matemáticas que rigen el espaciamiento planetario y el tiempo que tarda cada planeta en dar una vuelta alrededor del Sol.

En 1619, Kepler descubrió una relación básica para relacionar las órbitas de los planetas con sus distancias relativas al Sol. Definimos el periodo orbital de un planeta, (P), como el tiempo que tarda un planeta en dar una vuelta alrededor del Sol. Recordemos también que el semieje mayor de un planeta, a, es igual a su distancia media al Sol. La relación, ahora conocida como la tercera ley de Kepler, dice que el período orbital de un planeta al cuadrado es proporcional al semieje mayor de su órbita al cubo, o sea

P2∝a3
Cuando P (el periodo orbital) se mide en años y a se expresa en una cantidad conocida como unidad astronómica (UA), los dos lados de la fórmula no sólo son proporcionales, sino iguales. Una UA es la distancia media entre la Tierra y el Sol y equivale aproximadamente a 1,5 × 108 kilómetros. En estas unidades,

P2=a3
La tercera ley de Kepler se aplica a todos los objetos que orbitan alrededor del Sol, incluida la Tierra, y proporciona un medio para calcular sus distancias relativas al Sol a partir del tiempo que tardan en orbitar. Veamos un ejemplo concreto para ilustrar la utilidad de la tercera ley de Kepler.

Por ejemplo, supongamos que calculamos cuánto tarda Marte en dar una vuelta alrededor del Sol (en años terrestres). La tercera ley de Kepler permite calcular la distancia media de Marte al Sol. El período orbital de Marte (1,88 años terrestres) al cuadrado, o P2, es 1,882 = 3,53, y según la ecuación de la tercera ley de Kepler, es igual al cubo de su semieje mayor, o a3. ¿Qué número hay que elevar al cubo para obtener 3,53? La respuesta es 1,52 (ya que 1,52 × 1,52 × 1,52 = 3,53). Por tanto, el semieje mayor de Marte en unidades astronómicas debe ser 1,52 UA. En otras palabras, para dar una vuelta alrededor del Sol en algo menos de dos años, Marte debe estar aproximadamente a 50% (la mitad) de distancia del Sol que la Tierra.

EJEMPLO 3.1
Cálculo de períodos
Imagina que un objeto viaja alrededor del Sol. Cuál sería el periodo orbital del objeto si su órbita tiene un semieje mayor de 50 UA?

Solución
A partir de la tercera ley de Kepler, sabemos que (cuando utilizamos unidades de años y UA)

P2=a3
Si la órbita del objeto tiene un semieje mayor de 50 UA (a = 50), podemos elevar 50 al cubo y luego sacar la raíz cuadrada del resultado para obtener P:

PP=a3−−√=50×50×50−−−−−−−−−−−−√=125,000−−−−−−√=353.6years
Por tanto, el periodo orbital del objeto es de unos 350 años. Esto situaría a nuestro hipotético objeto más allá de la órbita de Plutón.

Compruebe su aprendizaje
¿Cuál sería el periodo orbital de un asteroide (un trozo rocoso entre Marte y Júpiter) con un semieje mayor de 3 UA?

RESPUESTA:
P=3×3×3−−−−−−−−−√=27−−√=5.2years
Las tres leyes del movimiento planetario de Kepler pueden resumirse como sigue:

Primera ley de Kepler: Cada planeta se mueve alrededor del Sol en una órbita que es una elipse, con el Sol en un foco de la elipse.
Segunda ley de Kepler: La línea recta que une un planeta y el Sol barre áreas iguales en el espacio en intervalos iguales de tiempo.
Tercera ley de Kepler: El cuadrado del periodo orbital de un planeta es directamente proporcional al cubo del semieje mayor de su órbita.
Las tres leyes de Kepler proporcionan una descripción geométrica precisa del movimiento planetario en el marco del sistema copernicano. Gracias a ellas, fue posible calcular las posiciones planetarias con gran precisión. Sin embargo, las leyes de Kepler son puramente descriptivas: no nos ayudan a comprender qué fuerzas de la naturaleza obligan a los planetas a seguir este conjunto particular de reglas. Ese paso se lo dejó a Isaac Newton.

EJEMPLO 3.2
Aplicación de la Tercera Ley de Kepler
Utilizando los períodos orbitales y los ejes semimayores de Venus y la Tierra que se proporcionan aquí, calcula P2 y a3, y verifica que obedecen a la tercera ley de Kepler. El período orbital de Venus es de 0,62 años y su semieje mayor es de 0,72 UA. El período orbital de la Tierra es de 1,00 año y su semieje mayor es de 1,00 UA.

Solución
Podemos utilizar la ecuación de la tercera ley de Kepler, P2 ∝ a3. Para Venus, P2 = 0,62 × 0,62 = 0,38 y a3 = 0,72 × 0,72 × 0,72 = 0,37 (el redondeo de los números a veces provoca pequeñas discrepancias como ésta). El cuadrado del período orbital (0,38) se aproxima al cubo del semieje mayor (0,37). Por tanto, Venus cumple la tercera ley de Kepler. Para la Tierra, P2 = 1,00 × 1,00 = 1,00 y a3 = 1,00 × 1,00 × 1,00 = 1,00. El cuadrado del período orbital (1,00) se aproxima (en este caso, es igual) al cubo del semieje mayor (1,00). Por lo tanto, la Tierra obedece la tercera ley de Kepler.

Compruebe su aprendizaje
Utilizando los períodos orbitales y los ejes semimayores de Saturno y Júpiter que se proporcionan aquí, calcula P2 y a3, y verifica que obedecen a la tercera ley de Kepler. El período orbital de Saturno es de 29,46 años y su semieje mayor es de 9,54 UA. El período orbital de Júpiter es de 11,86 años y su semieje mayor está a 5,20 UA.

RESPUESTA:
Para Saturno, P2 = 29,46 × 29,46 = 867,9 y a3 = 9,54 × 9,54 × 9,54 = 868,3. El cuadrado del período orbital (867,9) se aproxima al cubo del semieje mayor (868,3). Por lo tanto, Saturno obedece la tercera ley de Kepler.